


suivant: À propos de ce
Liste des projets
Chaque projet devra utiliser les outils Autoconf - Automake pour la compilation ainsi que LATEX pour la production du rapport. Un rapport unique par étudiant est demandé (Page de garde  (au minimum) deux pages de texte ; les codes sources peuvent être inclus dans les annexes). Vous pouvez vous inspirer du fichier se trouvant à l'adresse http://www.ai.univ-paris8.fr/~amsi/OD0405S1/dl/m_article.pdf pour la mise en page. Pour Autoconf - Automake, les fichiers NEWS, README, AUTHORS et ChangeLog doivent être renseignés.
(au minimum) deux pages de texte ; les codes sources peuvent être inclus dans les annexes). Vous pouvez vous inspirer du fichier se trouvant à l'adresse http://www.ai.univ-paris8.fr/~amsi/OD0405S1/dl/m_article.pdf pour la mise en page. Pour Autoconf - Automake, les fichiers NEWS, README, AUTHORS et ChangeLog doivent être renseignés.
1. Métro (deux étudiants maximum)
Créer un programme calculant le plus court chemin (en terme de nombre de stations parcourues) entre deux stations du métro parisien. La définition des lignes de métro est donnée dans un fichier texte, vous pouvez utiliser le fichier présent sur http://www.ai.univ-paris8.fr/~amsi/OD0405S1/dl/metro.data. Les intersections de lignes (les correspondances) seront calculées automatiquement (les correspondances avec changement du nom de la station sont données dans le fichier de metro.data). Le programme utilisera la Graphviz - Drawing Library pour générer le graphe du métro et exporter le rendu au format Postscript ; le plus court chemin demandé (par une interface texte) devra être mis en valeur par l'utilisation d'un autre code couleur par exemple.
2. Nombres premiers, 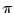 et
et 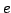 (un étudiant maximum)
(un étudiant maximum)
Écrire un programme calculant et affichant (suivant les options passées en argument) :
- la suite des nombres premiers entre
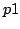 et
et 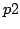 (arguments de la ligne de commandes) ;
(arguments de la ligne de commandes) ;
- la suite des décimales du nombre
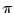 entre
entre 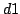 et
et 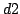 (arguments de la ligne de commandes) ;
(arguments de la ligne de commandes) ;
- la suite des décimales du nombre
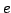 (
(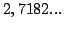 ) entre
) entre 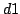 et
et 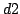 (arguments de la ligne de commandes).
(arguments de la ligne de commandes).
Utiliser, pour la gestion des grands nombres, la librairie GMP. La librairie et sa documentation se trouvent à l'adresse : http://gmplib.org/. Pour chaque problème, implémenter deux algorithmes au minimum. Comparer les différents algorithmes en produisant des graphiques GnuPlot des temps d'exécution sur des intervalles de plus en plus grands.
3. Le plus court chemin dans un labyrinthe (un étudiant maximum)
Écrire un programme qui génère aléatoirement des labyrinthes 1-connexes (il existe un et un seul chemin reliant deux points) de taille quelconque. Calculer, en utilisant l'algorithme de Dijkstra, le plus court chemin reliant deux points du labyrinthe. Le résultat obtenu sera rendu en Postscript (en vectoriel).
4. U.M.T.S. (deux étudiants maximum)
Vous avez à votre disposition une fonction qui génère un tableau linéaire représentant une image satellite carrée de largeur quelconque. Cette image est une carte des altitudes (256 niveaux) du terrain sur lequel une société de Télécoms souhaite placer 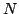 antennes de relais. Sachant que ces antennes ne couvrent qu'un rayon de
antennes de relais. Sachant que ces antennes ne couvrent qu'un rayon de 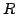 pixels et qu'elles n'émettent pas vers le haut, écrire le programme qui calcule le meilleur emplacement pour ces
pixels et qu'elles n'émettent pas vers le haut, écrire le programme qui calcule le meilleur emplacement pour ces 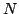 antennes de façon à obtenir la meilleure couverture possible. Le résultat obtenu sera rendu en Postscript (en pixmap pour la carte des altitudes et en vectoriel pour les antennes). Le générateur de cartes se trouve sur : http://www.ai.univ-paris8.fr/~amsi/OD0405S1/dl/plasma.c
antennes de façon à obtenir la meilleure couverture possible. Le résultat obtenu sera rendu en Postscript (en pixmap pour la carte des altitudes et en vectoriel pour les antennes). Le générateur de cartes se trouve sur : http://www.ai.univ-paris8.fr/~amsi/OD0405S1/dl/plasma.c
5. Jeu de Shannon (deux étudiants maximum)
Soit un graphe non dirigé et connexe à 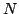 n
n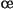 uds, dont deux n
uds, dont deux n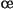 uds particuliers :
uds particuliers : 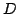 pour Départ et
pour Départ et 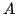 pour Arrivée. Deux joueurs, le lieur et le casseur peuvent alternativement modifier la structure du graphe. À chaque tour de jeu, le casseur casse une arête entre deux n
pour Arrivée. Deux joueurs, le lieur et le casseur peuvent alternativement modifier la structure du graphe. À chaque tour de jeu, le casseur casse une arête entre deux n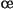 uds puis le lieur rend incassable une arête (non cassée) entre deux n
uds puis le lieur rend incassable une arête (non cassée) entre deux n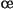 uds. Si, à un moment du jeu, il n'existe aucun chemin de
uds. Si, à un moment du jeu, il n'existe aucun chemin de 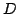 à
à 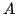 , le casseur a gagné. Si, à un moment donné, il existe un chemin incassable de
, le casseur a gagné. Si, à un moment donné, il existe un chemin incassable de 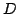 à
à 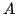 , le lieur a gagné.
, le lieur a gagné.
Écrire un programme utilisant la Graphviz - Drawing Library, qui permet de jouer contre la machine (interface texte ou graphique). Un compte-rendu devra être généré à la fin du jeu sous forme de plusieurs pages Postscript (une page par tour de jeu).
6. Arbre Généalogique (un étudiant maximum)
Créer un programme permettant la création d'arbres généalogiques. Ce programme utilisera la Graphviz - Drawing Library. Une interface texte servira à approvisionner la base de données (ex. un fichier) représentant l'arbre (un fichier par arbre). Nous pourrons, à tout moment, exporter l'arbre au format Dot ou Postscript.
7. Gestion de comptes bancaires (deux étudiants maximum)
Créer un logiciel de gestion de comptes banquaires. Chaque compte doit avoir un identifiant unique qui le lie à une personne (nom, prénom, adresse ...) ainsi qu'à une banque (identifiant, nom, adresse). Le logiciel doit effectuer et enregistrer toutes les opérations standards liées à un compte chèque : dépôt espèces ou chèque, virement émis ou reçu, paiement CB ou chèque, retrait CB et enfin ouverture ou fermeture de compte. Pour accéder à un compte, nous pouvons soit entrer directement son numéro, soit effectuer une recherche par nom (voir nom-prénom) afin d'obtenir les numéros de comptes correspondants. Nous pourrons, à tout moment, demander un historique complet (dates et natures des opérations suivies du solde du compte) des opérations effectuées sur un compte. Aussi, nous pourrons demander l'exportation d'un historique au format LATEX (inspirez-vous de vos relevés de compte banquaires pour la mise en page).
8. Mots croisés (deux étudiants maximum)
Partant d'un fichier «dictionnaire» contenant des lignes «mot : définition», nous souhaitons écrire un programme qui génère une grille de mots croisés de dimensions quelconques (l'utilisateur spécifiera les dimensions dans la ligne d'arguments du programme). À chaque exécution, la grille générée doit être (si possible) différente des précédentes. Le rendu devra être fait au format Postscript.



suivant: À propos de ce
Fares Belhadj
2004-11-23
(au minimum) deux pages de texte ; les codes sources peuvent être inclus dans les annexes). Vous pouvez vous inspirer du fichier se trouvant à l'adresse http://www.ai.univ-paris8.fr/~amsi/OD0405S1/dl/m_article.pdf pour la mise en page. Pour Autoconf - Automake, les fichiers NEWS, README, AUTHORS et ChangeLog doivent être renseignés.